The "No Shortcuts" Paradox
by Thomas Kühne
The Ancient Fallacy
The world has long been fooled by a certain Mr. Pythagoras whose Pythagorean theorem (c2=a2+b2, where c is the length of the hypotenuse in a right triangle and a & b are the lengths of the two legs) can be used to infer that the shortest distance s = √((x2-x1)2+(y2-y1)2) (also called the Euclidean distance) between two points P1=(x1,y1) & P2=(x2,y2) is shorter than the Manhattan distance m = h + v, where h = |x2-x1| and v = |y2-y1|, between the same two points.The Truth
The above suggests that the shortest distance s represents a shortcut in comparison to the path constructed by following |P1P| (h = |x2-x1|) and then |PP2| (v = |y2-y1|). However, nothing could be further from the truth. Apart from empirical results that show that shortcuts even result in prolonged traveling, it can be mathematically proven that the alleged shortcut |P1P2| with length s is exactly as long as the Manhattan distance h + v.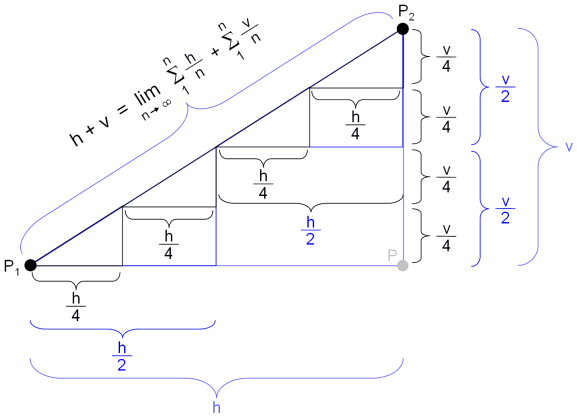
The Proof
Consider the above figure. The horizontal distance between P1 & P2 is h and the vertical distance v. The total distance between P1 and P2 via P hence is h + v. Let us start approximating the straight line between P1 and P2 by replacing the large triangle P1, P, P2 with two triangles where the legs have length h/2 and v/2 correspondingly (see above). A better approximation is obtained by using four triangles with leg lengths h/4 and v/4. The more triangles we use, the better the triangles will approximate the straight line between P1 and P2. In the limit, the leg lengths will be zero and the infinite number of triangles will match the straight line between P1 and P2. However, note that the sum of the horizontal distances — independently of the granularity of the division — is always h and the sum of the vertical distances is always v. As a result, the length of s is h + v as opposed to √(h2+v2) as commonly believed. Consequently, it does not matter whether one proceeds from P1 to P2 following a straight line or via P, the length of the path is always h + v. In other words, there are no shortcuts.The Fun Part
Hint: As is typical for a falsidical paradox, the above rationalization suggests a result that is not only counterintuitive but also wrong. The fun part is in figuring out where the flaw in the apparently logical reasoning is.Spoiler: Think about in what way the breaking up into small horizontal and vertical stretches constrains a particle moving along them.
